Autoregulation as a Network Motif

Random networks, finding patterns, and genes that regulate their own expression

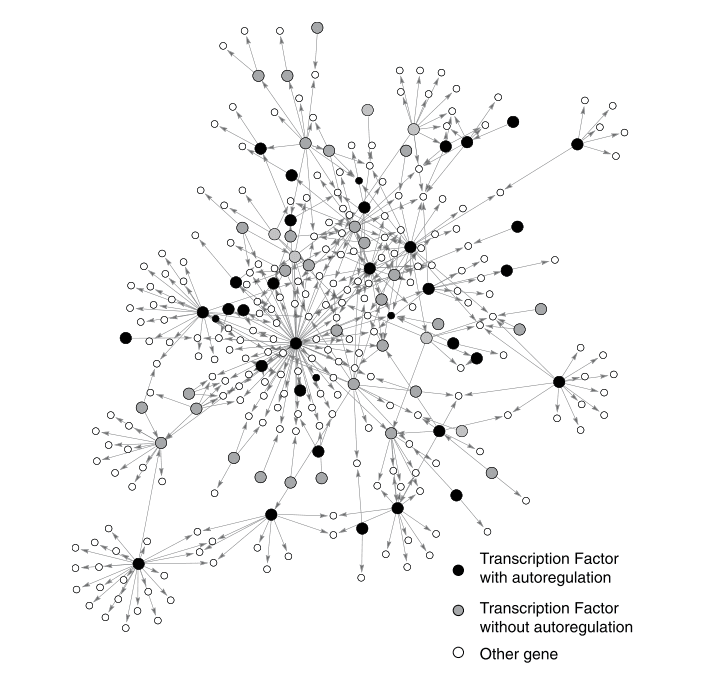
In the previous section, we looked at a single interaction in a transcription network X → Y, what it represents, and its dynamics. Now, let's look at an actual transcription network — the same one we introduced at the end of Part One: a network of about 20% of E.Coli's genes.

20% of E.Coli's transcription network, with the transcription factors split into ones with and without autoregulation. Taken from An Introduction to Systems Biology (Uri Alon, 2006)

Even with just 20% of the genes, the network looks pretty complex. In order to understand it, let's break it down into smaller networks and look for patterns — patterns that will hopefully help us understand the dynamics of the whole network.

Before we jump into breaking down this graph though, it's important to understand some context behind it.

The graph above is a snapshot in time. But cells, particularly bacterial ones, are a dynamic place. They divide. And mutate. In the right conditions, relentlessly and endlessly. As Uri Alon calculates in An Introduction to Systems Biologyi

A single bacterium placed in a test tube with 10 mL of liquid nutrient grows and divides to reach a saturating population of about 10 billion cells within less than a day. This population therefore underwent 10 billion DNA replications. Since the mutation rate is about one in a million per letter per replication, the population will include, for each letter in the genome, 10 different bacteria with a mutation in that letter. Thus, a change of any DNA letter can be rapidly reached in bacterial populations.

A single letter mutation in the DNA sequence of a promoter can prevent the usual binding of a transcription factor, and thus erase an arrow from the network. Similarly, mutations in the binding site, repositioning of DNA segments, or insertions of DNA from other sources (genetic recombination) can create new binding sites for transcription factors, and so, add arrows to the network.

Arrows, then, can be lost or added pretty easily and quite often. This means that pathways that are preserved across evolutionary timescales have to constantly be selected for against the random forces of mutations. In other words, if a pattern does emerge much more often than it would at random, then it must provide some evolutionary advantage to the organism. The loss of a pathway that's crucial for glucose metabolism, for example, would be detrimental to the cell's survival, so we're likely to see that pathway preserved in the network.

Random Networks and Network Motifs

Patterns that occur in a real network significantly more than they would at random are called network motifs. In order to determine this statistical significance, the real network needs to be compared to a random network; i.e. a network with the same parameters (number of nodes and arrows), but where the connections are assigned randomly.

There are a number of random network models, but we'll use the simplest one: the Erdős-Rényi (ER) model. The way it works is fairly simple: for every pair of nodes, the decision to connect them or not is made at random.

As an example, below is a comparison between a 'real' network and a random network for 14 nodes and 20 arrows (in mathematics, these 'arrows', or connections or pathways, are called edges). Try regenerating the random network to see different possibilities. Take note of the number of self-arrows — arrows that connect a node to itself — in the random one. How many are usually there, and how does it compare to the 'real' network? Later, we'll use the incidence of self-arrows as a starting point to compare networks and determine motifs.

Autoregulation

The self-arrows in the network denote a gene that regulates its own expression, a process known as autoregulation. In the E.coli transcription network image (reproduced below), the black circles represent transcription factor genes with autoregulation, and the grey circles represent transcription without.

20% of E.Coli's transcription network, with the transcription factors split into ones with and without autoregulation. Taken from An Introduction to Systems Biology (Uri Alon, 2006)

There are 40 autoregulatory transcription factors in this network. Thirty-four of these are repressers — proteins that repress their own expression: negative autoregulation.

Does autoregulation occur in this network significantly more often than it would at random? To answer that question, we'll need to compare it to the average number of self-arrows that would occur in an Erdős-Rényi network of the same size.

Let's say we have two nodes, and , and we start on node . There are two possible arrows: either it points to itself, or it points to . If we pick at random, the probability of a self-arrow is . If there are 3 nodes, then there are three possible arrows from , and the probability of a self-arrow is . Following this logic, if there are nodes, then the probability of a self arrow for any given node is:

The random network needs to have the same number of arrows as the real network for the comparison to be valid. Let's denote this number of arrows as . If the arrows are placed randomly, then the average number of self-arrows we'll get is just the number of arrows multiplied by the probability of a self-arrow, which gives:

and the standard deviation is approximately the square root of the mean, so:

For the E.coli network above, the number of nodes and arrows are and . Thus, the average number of self-arrows and its standard deviation are:

A random network with 424 nodes and 519 arrows expects only a little over 1 self-arrow. The real network, remember, has 40 self-arrows, which is about 35 standard deviations away from the expected value. That's a very high statistical significance.

Negative autoregulation itself, with 34 self-arrows, is about 30 standard deviations away. It's safe to say, then, that autoregulation, and in particular, negative autoregulation, is a network motif in transcription networks. Remember, earlier, we said that a network motif implies some evolutionary advantage — what's the advantage that negative autoregulation provides?

We'll explore this question in the next article. For now, feel free to play around with an Erdős-Rényi network generator below and see how the network changes when you change some parameters. You can also check it out in the Erdős-Rényi Graphs block.

If you liked this and would like to hear when new content is published, please subscribe below.

If you have any feedback, found bugs, or just want to reach out, feel free to DM me on Twitter or send me an email.